Системы координат — это математические модели, используемые для определения местоположения и ориентации объектов в пространстве. Они позволяют нам точно указывать на расположение объектов относительно друг друга и относительно некоторой точки. Системы координат особенно полезны в физике, географии, геодезии и компьютерной графике.
Наиболее распространенные системы координат — это декартова система координат, полярная система координат и сферическая система координат. Декартова система координат, также известная как прямоугольная система координат, использует оси x, y и z для определения местоположения объектов в трехмерном пространстве. Ось x указывает направление вперед и назад, ось y — направление влево и вправо, а ось z — направление вверх и вниз. III
Полярная система координат используется для определения местоположения объектов с помощью радиуса и угла. Она состоит из полярной оси, радиусного вектора и угла. Полярная система координат обычно используется для задания точек на плоскости или на сфере. В сферической системе координат местоположение точки определяется с помощью радиуса, полярного угла и азимутального угла. Она часто применяется в астрономии и физике.
Системы координат являются важным инструментом для измерения и анализа пространственных данных. Они позволяют нам точно определить местоположение и ориентацию объектов. Понимание того, как работают системы координат, может быть полезным не только в науке, но и в повседневной жизни.
Что такое системы координат?
Система координат состоит из осей и начала координат. Оси образуют прямоугольный перекресток, где каждая ось представляет собой линию, которая идет от начала координат. Начало координат обозначает точку, где пересекаются оси. В двумерной системе координат (ДПСК) обычно используется две оси — горизонтальная ось (ось X) и вертикальная ось (ось Y). В трехмерной системе координат дополнительно используется еще одна ось — ось Z.
Координаты точки в системе координат определяются с помощью чисел. На оси X положительные значения располагаются справа от начала координат, а отрицательные значения — слева. На оси Y положительные значения располагаются выше начала координат, а отрицательные значения — ниже. В трехмерной системе координат на оси Z положительные значения располагаются вверх, а отрицательные значения — вниз.
Системы координат широко используются в различных областях, таких как графика, физика, география и т. д. Они позволяют наглядно представить положение объектов и проводить различные математические операции с координатами.
Как работают системы координат?
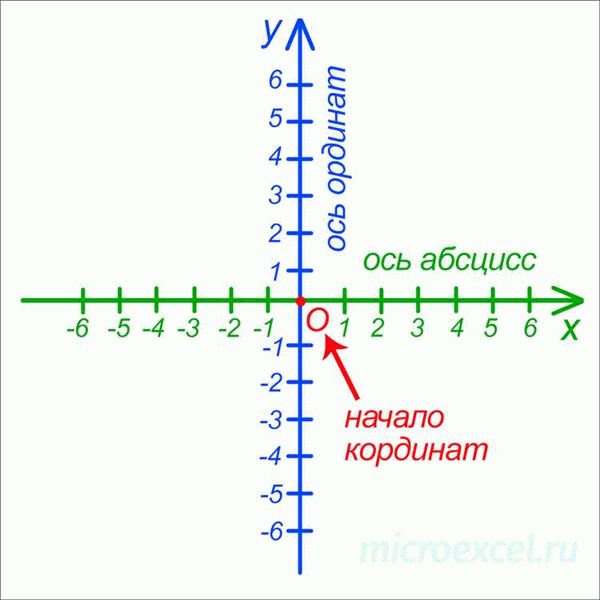
Одной из самых распространенных систем координат является декартова система координат (ДПСК). В ДПСК используются две перпендикулярные оси — горизонтальная ось x и вертикальная ось y. Основная точка, где оси пересекаются, называется началом координат и имеет координаты (0,0).
Для определения положения точки в ДПСК необходимо указать ее координаты. Например, точка A с координатами (2,3) находится в двух единицах вправо от начала координат и в трех единицах вверх от начала координат.
Системы координат используются в различных областях, таких как математика, физика, графика и дизайн. Они позволяют нам представлять и анализировать данные в удобной форме, что делает их незаменимыми инструментами для работы с пространственной информацией.
III ДПСК в пространстве: основные принципы
В трехмерной декартовой прямоугольной системе координат (III ДПСК) основная идея базируется на расширении двумерной системы координат до трех измерений. Это позволяет точнее и нагляднее описывать объекты и явления в трехмерном пространстве.
III ДПСК состоит из трех осей: X, Y и Z. Ось X направлена горизонтально вправо, ось Y — вертикально вверх, а ось Z — направлена вдоль наблюдателя, перпендикулярно плоскости XY. Таким образом, каждая точка в пространстве может быть определена с помощью трех координат: X, Y и Z.
В III ДПСК применяются аналогичные принципы относительно отображения графиков функций, систем уравнений и векторов, как и в двумерной системе координат. Кроме того, использование трех измерений позволяет более точно моделировать и описывать трехмерные объекты и явления в науке, инженерии, компьютерной графике и других областях.
Основные принципы III ДПСК включают в себя возможность определения расстояний между точками в пространстве, вычисление углов, определение площадей и объемов объектов, а также отображение сложных трехмерных объектов в виде графиков и диаграмм.
Использование III ДПСК позволяет работать с трехмерными данными более эффективно, точно и наглядно. Оно является неотъемлемой частью современных научных и инженерных исследований, а также применяется в различных компьютерных программных средах для моделирования и визуализации трехмерных объектов.
Как использовать III дпск в пространстве для решения задач?
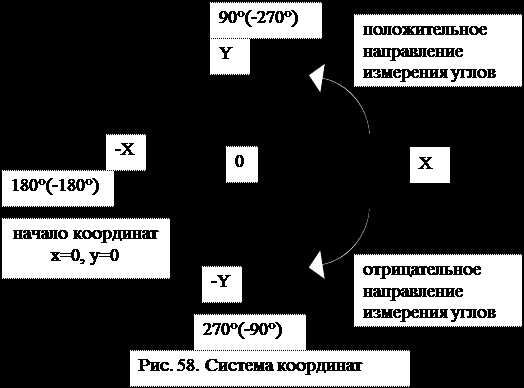
Использование III ДПСК в пространстве позволяет более точно определить положение объектов и решить различные задачи. Например, при моделировании физических объектов в трехмерном пространстве, III ДПСК позволяет определить положение объекта по его координатам и изменить его положение в соответствии с требованиями задачи.
Для решения задач на использование III ДПСК в пространстве необходимо определить начало координат (начало III ДПСК), оси координат (направление и отрицательное направление осей) и единицы измерения координат. Затем необходимо определить координаты точек и выполнять различные операции с этими координатами, такие как вычисление расстояния между точками, нахождение прямых и плоскостей, пересечение прямых и плоскостей и другие математические операции.
Использование III ДПСК в пространстве имеет широкий спектр применений, включая инженерию, архитектуру, компьютерную графику, физику и другие области. Поэтому знание и навыки работы с III ДПСК в пространстве являются важными для решения различных задач и задач моделирования в трехмерном пространстве.
Применение III ДПСК в пространстве в науке и технике
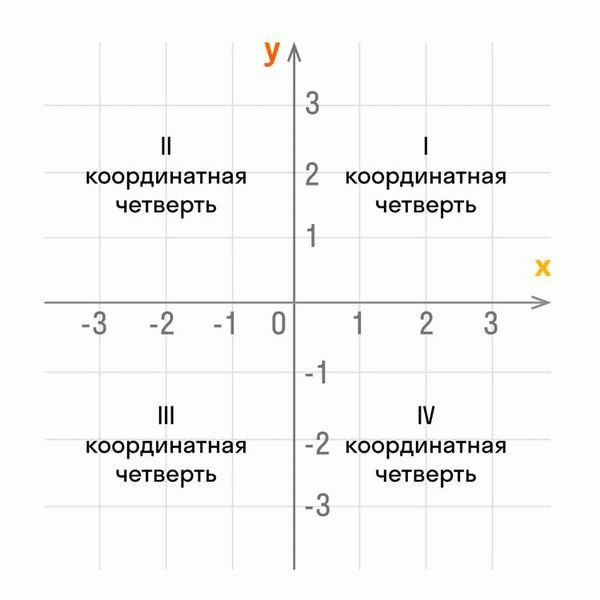
III ДПСК широко применяется в геодезии, аэрокосмической технике, робототехнике и других областях, где необходимо точно определить положение объектов в пространстве.
| Приложения III ДПСК в науке и технике | Примеры использования |
|---|---|
| Геодезия | Определение географических координат точек на Земле |
| Аэрокосмическая техника | Навигация и управление космическими аппаратами |
| Робототехника | Управление роботами в пространстве |
| Компьютерная графика | Определение координат для отображения трехмерных объектов на экране |
Использование III ДПСК позволяет представить пространственные объекты и явления в удобной форме и обеспечивает точность и надежность в решении различных научных и технических задач.
III дпск в пространстве и его роль в геодезии
III дпс (двухпараметрическая система координат) используется в геодезии для определения точного положения объектов в пространстве. Эта система координат имеет три оси: восток, север и вертикаль, и устанавливает связь между поверхностью Земли и глобальной системой координат (ГСК).
III дпс позволяет определить географическую широту, долготу и высоту точки. Для этого необходимы данные о времени, позиции спутника и эфемериды, которые предоставляют спутниковые системы. Координаты, определенные в III дпс, могут быть использованы для различных геодезических расчетов, таких как навигация, картография, определение перепада высот и других геодезических измерений.
Благодаря III дпс геодезисты могут точно определить положение объектов на Земле и производить высокоточные измерения. Эта система координат является важным инструментом для работы в геодезии и позволяет совершать сложные геодезические задачи с высокой точностью. III дпс в пространстве обеспечивает надежность и стабильность координатных данных, которые необходимы для обеспечения безопасности и эффективности различных геодезических работ.